Overview of AQA A-level Further Mathematics qualifications
Subject content:
Want to learn more about Advanced Level Qualifications (A-Levels) and how they can shape your academic future? Click here to explore: A-Level Information.
1. Overarching themes
A-level Further Mathematics specifications must require students to demonstrate overarching knowledge and skills from sections OT1, OT2, and OT3. These skills, along with mathematical thinking and understanding, must be applied throughout the detailed content in sections A to G.
| Theme | Content |
|---|---|
| OT1 Mathematical argument, language and proof | • Construct arguments using diagrams, graphs, logic, and accurate terminology (e.g., constant, function, variable). • Master mathematical language, syntax, and set theory. • Understand function definitions, domain, and range. • Critically analyze mathematical proofs and justifications. |
| OT2 Mathematical problem solving | • Identify the mathematical structure of a situation and simplify it to solve problems. • Develop extended arguments to tackle unstructured problems, including those in context. • Interpret and present solutions based on the original problem. • Understand the problem-solving cycle: defining the problem, gathering and processing information, and interpreting results, which may require revisiting the cycle. • Analyze and create diagrams, including those used in mechanics, to solve problems. |
| OT3 Mathematical modelling | • Convert real-world situations into mathematical models, using simplifying assumptions. • Use models with appropriate inputs to explore and engage with scenarios. • Interpret model outputs in the context of the original situation. • Recognize that models can be refined by assessing their outputs and assumptions, and evaluate their suitability. • Understand and apply modelling assumptions effectively. |
2. Compulsory content
| Section | Content |
|---|---|
| A: Proof | Construct proofs using mathematical induction, applied to contexts such as sums of series, divisibility, and powers of matrices. |
| B: Complex numbers | • Solve quadratic, cubic, and quartic equations with real coefficients. • Perform operations on complex numbers in the form x + iy and understand ‘real part’ and ‘imaginary part.’ • Utilize the complex conjugate and recognize that non-real roots occur in conjugate pairs. • Work with Argand diagrams. • Convert between Cartesian and modulus-argument forms of complex numbers. • Multiply and divide complex numbers in modulus-argument form. • Construct and interpret simple loci in the Argand diagram such as z – a > r and arg (z – a) = θ (knowledge of radians is assumed). • Apply de Moivre’s theorem for angle formulae and series sums. • Know and use the definition eiθ = cosθ + isinθ and the form z = reiθ • Find the n distinct n th roots of reiθ for r ≠ 0 and know that they form the vertices of a regular n -gon in the Argand diagram. • Solve geometric problems using complex roots of unity. |
| C: Matrices | • Add, subtract, multiply matrices; multiply by a scalar. • Use zero and identity matrices. • Represent 2D and limited 3D transformations with matrices. • Find invariant points/lines for transformations. • Calculate 2 x 2 and 3 x 3 determinants; interpret as scale factors. • Work with singular/non-singular matrices; calculate inverses. • Solve three simultaneous equations using inverse matrices. • Factorize determinants with row/column operations. • Find eigenvalues/eigenvectors; use the characteristic equation. • Diagonalisation of matrices; M = UDU-1; Mn = UD n U-1 ; when eigenvalues are real. |
| D: Further algebra and functions | • Understand roots and coefficients of polynomials up to quartic. • Form polynomials from transformed roots. • Apply summation formulas and method of differences. • Use and recognize Maclaurin series for common functions. • Solve limits, inequalities, and graph rational functions. • Sketch curves and apply transformations (translations, stretches, reflections, rotations). |
| E: Further calculus | • Solve improper integrals with undefined integrands or infinite ranges. • Derive volumes of revolution. • Compute the mean value of a function. • Use partial fractions for integration, including quadratic factors. • Differentiate inverse trigonometric functions. • Integrate using trigonometric substitutions. • Calculate arc length and surface area of revolution. • Apply reduction formulae for integration. • Evaluate limits for specific functions involving xk e-x and xklnx. |
| F: Further vectors | • Use vector and Cartesian forms for equations of straight lines and planes in 3D. • Calculate scalar products to find angles between lines, planes, and between a line and a plane. • Determine if vectors are perpendicular using the scalar product. • Calculate vector products and apply them to find triangle areas. • Use the equation (r – a) × b = 0 for straight lines. • Find intersections between two lines, and between a line and a plane. • Calculate perpendicular distances between two lines, a point and a line, and a point and a plane. |
| G: Polar coordinates | • Understand and convert between polar and Cartesian coordinates. • Sketch curves where 𝑟 is a function of θ, including trigonometric functions. • Calculate the area enclosed by a polar curve. |
| H: Hyperbolic functions | • Understand and define hyperbolic functions: sinh 𝑥, cosh 𝑥, tanh 𝑥, sech 𝑥, cosech 𝑥, and coth 𝑥, including domains, ranges, and graphing. • Differentiate and integrate hyperbolic functions. • Understand and use inverse hyperbolic functions, including their domains, ranges, and logarithmic forms. • Integrate functions of the form • Understand and use 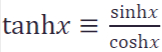 Understand and use cosh2x – sinh2x ≡ 1; sech2x ≡ 1 tanh2x; and cosech2 • Construct proofs using hyperbolic functions and identities. |
| I: Differential equations | • Find and use an integrating factor to solve differential equations of the form • Solve general and particular solutions of differential equations. • Apply differential equations in kinematics and other models. • Solve equations of the form y′′+ ay′+ by = 0 using auxiliary equations. • Solve y′′+ay′+by = f(x) by finding homogeneous solutions and adding particular integrals (when 𝑓(𝑥) is a polynomial, exponential, or trigonometric). • Understand how the discriminant of the auxiliary equation affects the solution form. • Solve simple harmonic motion equations and relate to motion. • Model damped oscillations and interpret light, critical, and heavy damping. • Solve coupled 1st-order equations in models like predator-prey dynamics. • Formulate differential equations using Hooke’s Law for harmonic motion. • Model damped motion with damping force proportional to velocity. |
| J: Numerical methods | • Mid-ordinate rule and Simpson’s rule for integration. • Euler’s step by step method for solving first order differential equations. • Improved Euler method for solving first order differential equations. yr+1 = yr−1 + 2hf (xr′ yr), xr+1 = xr + h |
3. Optional application 1 – mechanics
| Section | Content |
|---|---|
| MA: Dimensional analysis | • Determine dimensions of quantities and check dimensional consistency. • Predict formulae and identify variable powers in potential equations. |
| MB: Momentum and collisions | • Apply conservation of momentum in linear motion and vector cases, including resolving velocities. • Use the coefficient of restitution and Newton’s Experimental Law for direct collisions and impacts with a smooth surface. • Relate impulse to momentum using Ft = mv − mu, including resolving problems. • Calculate impulse for variable forces in one dimension using I = ∫ Fdt |
| MC: Work, energy and power | • Work done by a force in the direction or opposing motion, using WD = Fd cosθ • Gravitational potential energy applied to energy conservation problems. • Kinetic energy used in energy conservation problems. • Hooke’s Law including using modulus of elasticity. Use of • Work done by a variable force, using WD=∫ Fdx, also applied in conservation of energy problems. • Elastic potential energy using modulus of elasticity. Use of Use in conservation of energy problems. |
| MD: Circular motion | • Motion of a particle in a circle at constant speed (radians knowledge required). • Definition and use of angular speed in both radians and revolutions per time unit. • Relationships between speed, angular speed, radius and acceleration. Use of v = rω , a = rω2 and  . .• Apply vectors for position, velocity, and acceleration in circular motion. • Conical pendulum analysis with one or two strings. • Circular motion in a vertical plane, including conditions for completing vertical circles and applying conservation of energy. |
| ME: Centres of mass and moments | • Calculate the centre of mass for particle systems and composite bodies. • Determine the centre of mass of a lamina using integration. • Find centres of mass for bodies formed by rotating a region around the x -axis. • Analyze conditions for sliding and toppling, including problems involving suspension and inclined planes. • Use moments and couples to determine forces on a rigid body in equilibrium. |
4. Optional application 2 – statistics
| Section | Content |
|---|---|
| SA: Discrete random variables (DRVs) and expectation | • Understand discrete random variables (DRVs) presented as a table or function. • Calculate probabilities for DRVs. • Evaluate measures of central tendency and dispersion, including mean, variance, standard deviation, mode, and median. • Understand expectation and know the formulae: EX = ∑ xi pi ; EX2 = ∑ xi2 pi ; V arX = EX2 – (EX)2 • Understand expectation of linear functions of DRVs and know the formulae: EaX + b = aEX + b and V araX + b = a2Var (X) Know the formula EgX = ∑g (xi) pi Find the mean, variance and standard deviation for functions of a DRV such as E5X3, E18X-3, Var (6X -1) • Recognize and apply the discrete uniform distribution on the set {1, 2, …, n} and understand its use as a model. |
| SB: Poisson distribution | • Understand when a Poisson distribution is appropriate, denoted as X ~ Po(λ). • Use the Poisson formula or calculator function to find probabilities. • Know that the mean, variance, and standard deviation of a Poisson distribution are equal (mean = variance). • Understand the distribution of sums of independent Poisson distributions. • Conduct hypothesis tests on population means using Poisson probabilities from a single observation. |
| SC: Type I and Type II errors | • Understand and define Type I and Type II errors in context. • Calculate the probability of Type I errors for tests based on Poisson, Binomial, or normal distributions. • Understand the power of a test and calculate the probability of a Type II error (P(Type II error)) and test power for normal, Binomial, or Poisson-based tests. |
| SD: Continuous random variables (CRVs) | • Understand and use a probability density function (f(x)) for continuous distributions and differentiate between discrete and continuous distributions. • Work with distributions that are part discrete and part continuous. • Calculate the probability of an observation within a specified interval. • Determine the median and quartiles from a given probability density function (f(x)). • Find the mean, variance and standard deviation for a given pdf, f (x). Know the formulae EX = ∫ xfxdx , EX2 =∫ x2fxdx , VarX = EX2 – (EX)2 • Understand the expectation and variance of linear functions of CRVs and know the formulae: EaX + b = aEX + b and VaraX + b = a2Var (X) Know the formula EgX = ∫ gxf (x) dx Find the mean, variance and standard deviation of functions of a continuous random variable such as E5X3, E18X-3, Var (6X-1) • Understand and use a cumulative distribution function, F (x) . Know the relationship between f (x) and F (x). • Know that if X and Y are independent (discrete or continuous) random variables then EX + Y = EX + EY and VarX + Y = VarX+Var (Y) |
| SE: Chi squared tests for association | • Construct n × m contingency tables. • Use of 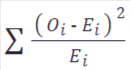 as an approximate χ2 statistic with appropriate degrees of freedom. as an approximate χ2 statistic with appropriate degrees of freedom.• Know and use the convention that all Ei • Identify sources of association based on the context. • Understand when and how to apply Yates’ correction. |
| SF: Exponential distribution | • Understand conditions for using the exponential distribution as a model, including its probability density function f (x) and cumulative distribution function F (x). • Calculate probabilities using F (x) or by integrating f (x). • Know and prove the mean, variance, and standard deviation of the distribution. • Recognize that intervals between Poisson events follow an exponential distribution. |
| SG: Inference – one sample t- distribution | Test for the mean of a normal distribution with unknown variance using a t with appropriate degrees of freedom. |
| SH: Confidence Intervals | • Construct symmetric confidence intervals for the mean of a normal distribution when variance is known. • For large samples with unknown variance, construct symmetric confidence intervals for the mean. • Make inferences based on confidence intervals provided or constructed. • For small samples with unknown variance, construct symmetric confidence intervals using the t-distribution. |
5. Optional application 3 – discrete mathematics
| Section | Content |
|---|---|
| DA: Graphs | • Understand key graph terminology: vertex, edge, trail, cycle, degree, subgraph, multiple edge, loop. • Identify or prove if a graph is Eulerian, semi-Eulerian, or Hamiltonian. • Apply Euler’s formula for connected planar graphs and use Kuratowski’s Theorem for planarity. • Work with complete, bipartite graphs, adjacency matrices, and graph complements. • Understand simple graphs, trees, and isomorphism between graphs. |
| DB: Networks | • Understand key network terminology: node, arc, and weight. • Solve optimization problems using spanning trees. • Address route inspection challenges. • Determine and interpret upper and lower bounds for the traveling salesperson problem. • Evaluate, modify, and refine network models. |
| DC: Network flows | • Interpret flow problems in directed arc networks. • Determine the value of a cut and its significance. • Utilize and understand the maximum flow-minimum cut theorem. • Incorporate supersources and supersinks into networks. • Augment flows to find the maximum flow in a network. • Address problems involving arcs with upper and lower capacity constraints. |
| DD: Linear programming | • Formulate constrained optimization problems. • Solve these problems using graphical methods. • Apply the Simplex algorithm for optimizing (maximizing or minimizing) an objective function, including the use of slack variables. • Interpret the Simplex tableau. |
| DE: Critical path analysis | • Construct and interpret a precedence network using activity-on-node representation. • Determine earliest and latest start and finish times for activities within the network. • Identify critical activities, critical paths, and the float for non-critical activities. • Refine models to understand the implications of changes in critical path analysis. • Construct and interpret Gantt charts and resource histograms. • Perform resource leveling using heuristic procedures to address resource restrictions. |
| DF: Game theory for zero-sum games | • Understand and construct pay-off matrices. • Determine play-safe strategies and the game’s value. • Prove the existence or non-existence of stable solutions. • Identify and utilize dominated strategies. • Calculate optimal mixed strategies using graphical methods. • Convert higher-order games into linear programming problems for solution. |
| DG: Binary operations | • Apply binary operations, including modular arithmetic and matrix multiplication. • Prove commutativity and associativity. • Construct Cayley tables for binary operations. • Establish the identity element and find inverses within sets. • Use group terminology: order, period, subgroup, trivial, and non-trivial. • Apply group axioms: closure, identity, inverses, and associativity. • Recognize finite and infinite groups, including symmetry and cyclic groups. • Understand and apply Lagrange’s theorem and group generators. • Identify isomorphisms between finite-order groups. |
If you need help with Further Mathematics or any other subject, our tutors are ready to support you on your academic journey. Don’t miss your chance to succeed—take a trial lesson today!
Assessment
| Component | Content | Questions | Final score | Weighting of final grade |
|---|---|---|---|---|
| Paper 1 | May assess content from the following sections: A: Proof B: Complex numbers C: Matrices D: Further algebra and functions E: Further calculus F: Further vectors G: Polar coordinates H: Hyperbolic functions I: Differential equations J: Numerical methods | A mix of question styles, from short, single-mark questions to multi-step problems. | 100 marks | 33⅓% of A-level |
| Paper 2 | May assess content from the following sections: A: Proof B: Complex numbers C: Matrices D: Further algebra and functions E: Further calculus F: Further vectors G: Polar coordinates H: Hyperbolic functions I: Differential equations J: Numerical methods | A mix of question styles, from short, single-mark questions to multi-step problems. | 100 marks | 33⅓% of A-level |
| Paper 3 | One question paper answer booklet on Discrete and one question paper answer booklet on Statistics. OR One question paper answer booklet on Statistics and one question paper answer booklet on Mechanics. OR One question paper answer booklet on Mechanics and one question paper answer booklet on Discrete. | A mix of question styles, from short, single-mark questions to multi-step problems. | 100 marks | 33⅓% of A-level |
Weighting of assessment objectives for A-level Further Mathematics
Exams will assess students on the following objectives:
AO1: Use and Apply Standard Techniques:
– Accurately execute routine procedures.
– Recall relevant facts and definitions.
AO2: Reason, Interpret, and Communicate Mathematically:
– Construct rigorous mathematical arguments, including proofs.
– Make deductions and assess argument validity.
– Clearly explain reasoning using proper mathematical language.
AO3: Solve Problems Within Mathematics and in Other Contexts:
– Translate problems into mathematical processes.
– Interpret solutions within context and evaluate their accuracy.
– Develop and use mathematical models.
– Assess model outcomes, recognizing limitations and suggesting improvements.
| Assessment objectives AOs* | Component Paper 1 (%) | Component Paper 2 (%) | Component Paper 3 (%) | Overall Weighting (%) |
|---|---|---|---|---|
| AO1 | 55 | 55 | 40 | 50 |
| AO2 | 25 | 25 | 25 | 25 |
| AO3 | 20 | 20 | 35 | 25 |
| Overall weighting of components | 33 ⅓ | 33 ⅓ | 33 ⅓ | 100 |
Assessment weightings
The marks awarded on the exam papers will be adjusted to align with the component weightings. Final marks are calculated by adding these scaled marks for each component. Grade boundaries will be determined based on the total scaled mark. The scaling and total scaled marks are outlined in the table provided.
| Сomponent | Maximum raw mark | Scaling factor | Maximum scaled mark |
|---|---|---|---|
| Paper 1 | 100 | ×1 | 100 |
| Paper 2 | 100 | ×1 | 100 |
| Paper 3 | 100 | ×1 | 100 |
| Total scaled mark: | 300 |